Maxima
Maxima CAS jest to program do obliczeń symbolicznych i numerycznych.
Przykładowe zadania z rozwiązaniami w programie Maxima CAS (wxMaxima wersja 0.7.1, Maxima 5.13.0, GNU Common Lisp GCL 2.6.8)
instalacja
edytuj- Ubuntu[1]
Input czyli wprowadzanie poleceń
edytujKażde wprowadzone polecenie kończymy średnikiem ; bądź symbolem dolara $
Zakończenie polecenia średnikiem powoduje, że Maxima oblicza wyrażenie i wyświetla wynik jego działania:
(%i1) 2*2; (%o1) 4
Zakończenie polecenia symbolem dolara $ powoduje, że Maxima oblicza wyrażenie, przechowuje jego wynik (w tym przykładzie zapisany w %o2) lecz nie wyświetla go:
(%i2) 2*2$ (%i3)
Wynik jest dostępny zmienną % (ostatni obliczony wynik)
(%i3)%; (%o3) 4
bądź, w naszym przypadku, %o2
(%i4)%o2; (%o4) 4
Wyjątki : Wewnątrz instrukcji block polecenia kończy się przecinkiem, oprócz ostatniego, które nie ma swojego końcowego znaku.
Przebieg i struktura programu
edytuj
Interpreter Maximy przyjmuje:
- pojedyncze proste polecenie (1 linia)
- polecenie złożone (wiele linii)
- programy, czyli pliki wsadowe zawierające polecenia. Są to pliki tekstowe (ANSI,UTF-8) z rozszerzeniem mac. Otwieramy np. przez Menu/File/Batch file,
- moduły z definicjami funkcji ( package ) napisane w Maximie (*.mac) lub Lispie ( *.lisp) za pomocą funkcji load lub z Menu ( load package )
Przykład prostego polecenia, nadajemy zmiennej a wartość 2 :
a:2;
Jak widać Maxima wykorzystuje znak dwukropka dla nadania wartości
Przykład pliku wsadowego (możemy go zapisać jako np. a.mac):
/* zawartość pliku wsadowego zawierającego program z rozszerzeniem mac */ i:1; block ( loop, i:i+1, if i<100 then go(loop) ); i;
Przykłady ładowania modułu:
(%i2) load("complex_dynamics.lisp");
(%o2) C:/PROGRA~1/MAXIMA~1.2/share/maxima/5.19.2/share/dynamics/complex_dynamics.lisp
lub
(%i1) load("dynamics");
(%o1) C:/PROGRA~1/MAXIMA~1.2/share/maxima/5.19.2/share/dynamics/dynamics.mac
blok
edytujblock ([v_1, …, v_m], expr_1, …, expr_n) block (expr_1, …, expr_n) ( expr_1, expr_2,... , expr_n );
Uwagi:
- w ostatniej linii bloku nie ma znaku końca linii
- zmienne lokalne można deklarować tylko w bloku rozpoczynającym się od słowa kluczowego block[2]
Struktury
edytuj- listy
- tablice
- declared: flonum, fixnum,
- hashed
- macierze
Róznica pomiędzy
- tablicami a macierzami[3]
Tablice
edytuj(%i1) array(a,3); (%o1) a (%i2) a[0]; (%o2) a[0] (%i3) a[3]; (%o3) a[3] (%i4) a[4]; Array a has dimensions [3], but was called with [4] -- an error. To debug this try: debugmode(true); (%i5) a[0]:1; (%o5) 1
Liczby
edytujLiczby losowe
edytujbfloat(random(10^fpprec) / 10^fpprec); /* random bfloat with fpprec decimal digits in the range 0 to 1 */
Liczby całkowite
edytujLiczby rzeczywiste
edytujLiczby zmiennoprzecinkowe
edytujLiczby dziesiętne ( float) są standardowo wyświetlane z precyzją 16 cyfr dziesiętnych:
(%i1) fpprec; (%o1) 16 (%i2) fpprintprec; (%o2) 0
(%i3) float(%pi); (%o3) 3.141592653589793
Zmian precyzji
Standardowo fpprec jest równy 16. Możemy zwiększyć fpprec:
fpprec:100;
ale nie wpływa to na obliczenia na liczbach float tylko na bfloat.
W wxMaximie
bfloat(%pi),fpprec:1000;
dodatkowo zmieniamy display2d na true, aby wyświetlić wszystkie cyfry (w konsolowej wersji , tj. Maximie nie trzeba tego robić)
bfloat(%pi),fpprec:1000; (%o5) 3.1415926535897932384626433832795028841971693993751058209749445923078164\ 062862089986280348253421170679821480865132823066470938446095505822317253594081\ 284811174502841027019385211055596446229489549303819644288109756659334461284756\ 482337867831652712019091456485669234603486104543266482133936072602491412737245\ 870066063155881748815209209628292540917153643678925903600113305305488204665213\ 841469519415116094330572703657595919530921861173819326117931051185480744623799\ 627495673518857527248912279381830119491298336733624406566430860213949463952247\ 371907021798609437027705392171762931767523846748184676694051320005681271452635\ 608277857713427577896091736371787214684409012249534301465495853710507922796892\ 589235420199561121290219608640344181598136297747713099605187072113499999983729\ 780499510597317328160963185950244594553469083026425223082533446850352619311881\ 710100031378387528865875332083814206171776691473035982534904287554687311595628\ 63882353787593751957781857780532171226806613001927876611195909216420199b0
Moduł: floatproperties
(%i1) load(floatproperties); (%o1) "/usr/local/share/maxima/5.31.3/share/contrib/floatproperties.lisp"
pozwala sprawdzić właściwości liczb.
Liczby zespolone
edytujLiczby zespolone w postaci graficznej [4]
Postać algebraiczna (kanoniczna) c:x+y*%i
(%i1) c:5+3*%i; (%o1) 3*%i+5
część rzeczywista:
(%i2) x:realpart(c); (%o2) 5
część urojona:
(%i3) y:imagpart(c); (%o3) 3
Moduł:
(%i4) r:float(abs(c)); (%o4) 5.830951894845301;
Argument:
(%i5) t:float(carg(c)); (%o5) 0.54041950027058;
Postać wykładnicza:
(%i10) c1:r*%e^(%i*t); (%o10) sqrt(34)*%e^(%i*atan(3/5))
Powrót do formy algebraicznej:
(%i11) rectform(%); (%o11) 3*%i+5
Postać trygonometryczna:
(%i32) c2:r*(cos(t)+%i*sin(t)); (%o32) 5.830951894845301*((3*%i)/sqrt(34)+5/sqrt(34))
Powrót do formy algebraicznej:
(%i33) rectform(%); (%o33) (17.4928556845359*%i)/sqrt(34)+29.1547594742265/sqrt(34) (%i34) float(%), numer; (%o34) 3.0*%i+4.999999999999999
Porównywanie dwóch liczb zespolonych:
(%i12) IsEqual(c1,c2,eps):=
if abs(realpart(c1)-realpart(c2))<=eps
and
abs(imagpart(c1)-imagpart(c2))<=eps
then true
else false;
Sprawdzamy działanie funkcji:
(%i13) IsEqual(1.1, 1.27, 0.1); (%o13) false
Pierwiastek kwadratowy
csqrt(z):= block( [t,w,re,im], t:abs(z)+realpart(z), if t>0 then (re:sqrt(t/2), im:imagpart(z)/sqrt(2*t)) else (im:abs(z), re:0), w:re+im*%i, return(w) )$
Sortowanie listy liczb zespolonych wg argumentu:
l2_ordered: sort(l2, lambda([z1,z2], is(carg(z1) < carg(z2))))$
konwersje
edytujUżycie funkcji prinf:
Radius: 0.00001$
sRadius : printf(false,"~f",Radius);
print("Radius =", Radius, " = ", sRadius);
daje wynik
Radius = 1.0E-5 = 0.00001
Funkcje
edytujtypy:
- prosta
- rekurencyjna
- anonimowa (lambda expression = an anonymous function)
definicja
edytujDefiniuj funkcje matematyczne za pomocą:
- procedury:
define() - operatora definicji funkcji
:=
Różnica:
- operatora definicji funkcji nigdy nie ewaluuje ciała funkcji (wyjątek ewaluacja za pomocą quote-quote = )[5]
- procedura define zawsze ewaluuje ciało funkcji (chyba że jest wyłączone = explicitly quoted). "[6]
| Funkcje matematyczne definiuj zawsze za pomocą define() |
Definicja prostej funkcji:
(%i1) f(z,c):=z*z+c; (%o1) f(z,c):=z*z+c
Jej pierwszej pochodnej względem zmiennej z:
(%i2) m(z,c):=diff(f(z,c),z,1);
lub lepiej:
define(m(z,c), diff(f(z,c),z,1));
Sprawdzamy wzór pochodnej:
(%i3) m(z,c); (%o3) 2*z
Definicja funkcji rekurencyjnej:
(%i12) F(n, z, c) :=
if n=1 then f(z,c)
else f(F(n-1, z, c),c);
(%o12) F(n,z,c):=if n=1 then f(z,c) else f(F(n-1,c,z),c)
Sprawdzamy wzór:
(%i13) F(2,z,c); (%o13) (z^2+c)^2+c
map
edytujDefiniujemy funkcję:
define(f(z), z^2); f(z):=z^2
sprawdzamy:
fundef(f(z)); fundef: no such function: f(z) -- an error. To debug this try: debugmode(true);
poprawne użycie fundef (tylko nazwa funkcji):
fundef(f); f(z):=z^2
Wprowadzamy przykładową listę:
s:[z=1,z=2]; [z=1,z=2]
Stosujemy funkcję f do wszystkich elementów listy s:
map(f,s); [z^2=1,z^2=4]
maplist(f,s); [z^2=1,z^2=4]
Usuwamy lewą stronę elementów listy:
s:map(rhs,s); [1,4]
Teraz ponownie stosujemy funkcję f:
map(f,s); [1,4]
maplist(f,s); [1,4]
Zmienne lokalne funkcji
edytujPamiętaj że zmienne lokalne musisz zadeklarować przed użyciem (porównaj konstrukcje w Lispie).
give_circle(center,radius,n_points):=block( [t,dt,x,y,xy], /* deklaracja */ t:0, dt:(2*%pi)/n_points, x:realpart(center)+radius*cos(t), y:imagpart(center)+radius*sin(t), xy:makelist ([x,y], k, 1, 1), for i:1 thru (n_points-1) step 1 do ( t:t+dt, x:realpart(center)+radius*cos(t), y:imagpart(center)+radius*sin(t), xy:cons([x,y],xy) ), return(xy) );
Tak używamy tej funkcji:
center:0; radius:1; n_points:10; xy:give_circle(center,radius,n_points); load(draw); draw2d( points(xy))$
Porównaj ten kod z:
n_points:1000; dt:(2*%pi)/n_points; t:0*%pi; /* compute coordinates or root point */ x:cos(t); y:sin(t); /* save coordinates to list*/ xy:makelist ([x,y], i, 1, 1); for i:1 thru (n_points-1) step 1 do ( t:t+dt, x:cos(t), y:sin(t), xy:cons([x,y],xy) ); load(draw); draw2d( points(xy))$
Kompilacja
edytujFunkcje możemy skompilować. Wtedy szybciej działają:
compile(all);
mode_declare (y_1, mode_1, …, y_n, mode_n)
gdzie:
- y_n jest zmienną lub funkcją
- mode_n jest typem zmiennej lub funkcji
Kompilacja z mode_declare:[7]
- jest korzystna gdy funkcja wykonuje istotne obliczenia, szczególnie numeryczna
- nie przynosi korzyści gdy większość czasu wykonuje wbudowane funkcje Maximy (skompilowany kod Lispa) takie jak: realroots, expand, ratsimp, etc.
Rodzaje typów mode:
- boolean
- fixnum
- number
- rational
- float.
Rozwiązywanie równań
edytujSprawdzamy:
plot_options;
wynik:
[[plot_format, gnuplot_pipes]]
Pojedyncze równanie
edytujChcemy znaleźć punkty okresowe dla funkcji Fc(z)=z*z+c dla c=0+1*i (z i c są liczbami zespolonymi).
W tym celu najpierw określamy wartość c:
(%i1) c:1*%i; (%o1) %i
Okres=1 (punkty stałe)
edytujRozwiązujemy:
(%i7) p:float(rectform(solve([z*z+c=z],[z]))); (%o7) [z=0.62481053384383*%i-0.30024259022012,z=1.30024259022012-0.62481053384383*%i]
Szukamy punktu odpychającego (źródło, repeller), czyli beta:
if (abs(2*rhs(p[1]))<1)
then block(
beta:rhs(p[1]),
alfa:rhs(p[2])
)
else block(
alfa:rhs(p[1]),
beta:rhs(p[2])
);
Pokazujemy punkt stały typu alfa:
(%i20) alfa; (%o20) 0.62481053384383*%i-0.30024259022012
Pokazujemy punkt stały typu beta:
(%i21) beta; (%o21) 1.30024259022012-0.62481053384383*%i
Pokazujemy, że suma alfa i beta jest równa 1
(%i10) p:solve([z*z+c=z], [z]); (%o10) [z=-(sqrt(1-4*%i)-1)/2,z=(sqrt(1-4*%i)+1)/2] (%i14) s:radcan(rhs(p[1]+p[2])); (%o14) 1
Rysujemy punkty:
(%i15) xx:makelist (realpart(rhs(p[i])), i, 1, length(p)); (%o15) [-0.30024259022012,1.30024259022012] (%i16) yy:makelist (imagpart(rhs(p[i])), i, 1, length(p)); (%o16) [0.62481053384383,-0.62481053384383] (%i18) plot2d([discrete,xx,yy], [style, points]);
Można dodać też punkt z=1/2 (alfa i beta są symetryczna względem 1/2):
(%i31) xx:cons(1/2,xx); (%o31) [1/2,-0.30024259022012,1.30024259022012] (%i34) yy:cons(0,yy); (%o34) [0,0.62481053384383,-0.62481053384383] (%i35) plot2d([discrete,xx,yy], [style, points]);
Punkty o okresie = 2
edytuj(%i2) solve([(z*z+c)^2+c=z], [z]); (%o2) [z=-(sqrt(-4*c-3)+1)/2,z=(sqrt(-4*c-3)-1)/2,z=-(sqrt(1-4*c)-1)/2,z=(sqrt(1-4*c)+1)/2]
Pokazujemy że z1+z2 = -1
(%i4) s:radcan(rhs(p[1]+p[2])); (%o4) -1
Pokazujemy że z2+z3=1
(%i6) s:radcan(rhs(p[3]+p[4])); (%o6) 1
Punkty o dowolnym okresie
edytuj(%i41) giveRoots(period,c):=allroots(%i*F(period,z,c)); (%o41) giveRoots(period,c):=allroots(%i*F(period,z,c))
Metoda Newtona
edytujload (newton1);
definiujemy równanie:
eq1:z^3-1;
szukamy pojedynczego rozwiązania w okolicy %i:
s:newton(eq1,z,%i,0.1);
otrzymujemy:
(%o19) -(0.33333333333333*((-(0.33333333333333*((%i+0.33333333333333*(-%i-1))^3-1))/(%i+0.33333333333333*(-%i-1))^2+%i +0.33333333333333*(-%i-1))^3-1)) /(-(0.33333333333333*((%i+0.33333333333333*(-%i-1))^3-1))/(%i+0.33333333333333*(-%i-1))^2+%i+0.33333333333333*(-%i-1))^2 -(0.33333333333333*((%i+0.33333333333333*(-%i-1))^3-1))/(%i+0.33333333333333*(-%i-1))^2+%i+0.33333333333333*(-%i-1)
zmieniamy formę wyniku:
s1:rectform(float(s));
otrzymujemy :
0.86816551188735*%i-0.50879080328932
Układ równań
edytujliniowych
edytuj
solve([2x-3=0,x-y=0],[x,y])
nieliniowych
edytujUkład równań nieliniowych rozwiązujemy za pomocą komendy algsys (przykłady Stavrosa Macrakisa). Wynik zależy co uznamy za parametr a co za zmienną.
(%i2) algsys([a*x+y=3,x+b*y=1],[x,y]); (%o2) [[x=(3*b-1)/(a*b-1),y=(a-3)/(a*b-1)]]
(%i3) algsys([a*x+y=3,x+b*y=1],[a,b]); (%o3) [[a=-(y-3)/x,b=-(x-1)/y]]
(%i4) algsys([a*x+y=3,x+b*y=1],[x,b]); (%o4) [[x=-(y-3)/a,b=(y+a-3)/(a*y)]]
(%i5) algsys([a*x+y=3,x+b*y=1],[y,a]); (%o5) [[y=-(x-1)/b,a=(x+3*b-1)/(b*x)]]
Jeśli liczba równań jest mniejsza niż liczba zmiennych to wynikiem będzie równanie parametryczne
(%i1) algsys([a*x+y=3,x+b*y=1],[a,b,x,y]); (%o1) [[a=(3*%r1-%r1*%r2)/(%r1*(1-%r1*%r2)),b=%r1,x=1-%r1*%r2,y=%r2]]
Przykład 1:
edytujRozwiązywanie układu równań: Definiujemy pierwsze równanie:
(%i1) z*z+c=z; (%o1) z^2+c=z
Definiujemy drugie równanie (t jest to kąt w obrotach; 1 obrót = 360 stopni):
(%i2) 2*z=%e^(2*t*%pi*%i); (%o2) 2*z=%e^(2*%i*%pi*t)
Ponieważ 2 równanie ma tylko 1 zmienną eliminujemy zmienną z pierwszego równania:
(%i3) eliminate([%i1,%i2],[z]); (%o3) [%e^(4*%i*%pi*t)-2*%e^(2*%i*%pi*t)+4*c]
Rozwiązujemy równanie %o3 względem zmiennej c:
(%i4) solve([%e^(4*%i*%pi*t)-2*%e^(2*%i*%pi*t)+4*c], [c]); (%o4) [c=-(%e^(4*%i*%pi*t)-2*%e^(2*%i*%pi*t))/4]
Definiujemy funkcję :
(%i34) define(c1(t),rhs(s[1])); (%o34) c1(t):=-(%e^(4*%i*%pi*t)-2*%e^(2*%i*%pi*t))/4
Sprawdzamy działanie:
(%i35) c1(0); (%o35) 1/4
Rysujemy wykres (główny komponent zbioru Mandelbrota):
plot2d ([parametric, realpart(c1(t)), imagpart(c1(t)), [t,0,2*%pi],[nticks,2000]])$
Rysowanie
edytuj"Maxima-draw is broken in Ubuntu 16.04 due to a change in the GCL lisp compiler. At present, the only workaround I know is to compile Maxima yourself. I have compiled it in my Xubuntu 16.04 with SBCL instead of GCL and it works as expected." Mario Rodriguez
funkcje
edytujRysowanie 1 funkcji
edytujDefinicja funkcji f1:
f1(x):=a*x*(1-x)$
Rysowanie funkcji y:=f1(x) w zakresie 0 <= x <= 1:
plot2d(f1(x),[x,0,1]);
inny sposób:
load(draw); draw2d(explicit(x,x,-1,1));
Topologiczny sinus:
plot2d (sin(1/x), [x, 0, 1])$
Rysowanie kilku funkcji na 1 wykresie
edytujDefinicja funkcji f1:
f1(x):=%pi/2;
Definicja funkcji f2:
f2(x):=-%pi/2;
Rysowanie:
plot2d([f1(x),f2(x),atan(x)],[x,-5,5],[plot_format, gnuplot]);

Inny przykład:
plot2d([round(x),x,x*x,floor(x),ceiling(x),1/x,log(x)], [x,0,5],[y,0,5],[plot_format, gnuplot])$
plot2D
edytujDla niektórych funkcji f(x) typowa instrukcja:
plot2d (f(x), [x, 0, 1])
działa prawidłowo, dla innych daje błąd[8].
Rozwiązaniem jest wywołanie funkcji w postaci: '(f(x)) w liście argumentów plot2d. Przykłady:
f(x) := if x > 1 then 2/(x^2+1) else x^2$
plot2d ('(f(x)), [x, 0, 3])$
g(x) := quad_qag (t^2, t, 0, x, 2) [1]$
plot2d ('(g(x)), [x, -2, 2])$
W tych przykładach, jeśli użyjemy f(x) and g(x) bez znaku ' to pojawi się błąd.
Proszę zwrócić uwagę:
'(f(x))
nie
'f(x).
Rysowanie funkcji 2 zmiennych
edytujplot3d(atan2(y,x), [x,-5,5], [y,-5,5], [plot_format,gnuplot])$

Wektory
edytuj
ODE
edytuj- dokumentacja - Maxima by Example: Ch. 3, Ordinary Differential Equation Tools by Edwin L. Woollett December 21, 2017
Figury
edytujkoło
edytujRysujemy koło o promieniu =1 i środku = 0
- gotowa funkcja z draw:
/* circle https://math.stackexchange.com/questions/588180/how-to-plot-circle-with-maxima/588621#588621 */
nticks = 100,
fill_color = white,
color = gray,
transparent = true,
line_width = 5,
ellipse (realpart(Center), imagpart(Center), Radius, Radius, 0, 360),
- w postaci biegunowej:
load(draw); draw2d(polar(1,theta,0,2*%pi));
- w postaci parametrycznej:
plot2d ([parametric, cos(t), sin(t), [t,-%pi,%pi],[nticks,80]], [x, -4/3, 4/3])$
- w postaci uwikłanej
load(implicit_plot); z:x+y*%i; implicit_plot (abs(z) = 1, [x, -4, 4], [y, -4, 4]);
- za pomocą listy punktów połączonych liniami. Gdy pierwszy i ostatni punkt listy jest taki sam to otrzymujemy krzywą zamkniętą
/*
Batch file for Maxima CAS
save as a s.mac
run maxima :
maxima
and then :
batch("s.mac");
*/
kill(all);
remvalue(all);
/* ---------- functions ---------------------- */
/* converts complex number to the draw format */
d(z):=[float(realpart(z)), float(imagpart(z))];
/*
point of the unit circle D={w:abs(w)=1 } where w=l(t)
t is angle in turns
1 turn = 360 degree = 2*Pi radians
*/
l(t):= float(rectform(%e^(%i*t*2*%pi)));
/* circle point */
cl(center, radius, t) := center + radius*l(t);
/* here t maybe real number */
GiveCircleArc(center, radius, tmin, tmax, n):=(
[t, dt, list, i],
dt : (tmax - tmin)/n,
/* add first turn */
t : tmin,
z: cl(center, radius, t),
list : [z],
/* add arc turns */
while t < tmax do
( t: t + dt,
z: cl(center, radius, t),
list : endcons(z, list)),
/* add last turn */
t : tmax,
z: cl(center, radius, t),
list : endcons(z, list),
/* to draw format */
list : map(d, list)
)$
compile(all);
arc1 : GiveCircleArc( 0, 1, 0, 1/2, 10)$
arc2 : GiveCircleArc(-1, 1, 1/2, 1, 10)$
/* ---------------- draw ------------------------------- */
path:""$ /* if empty then file is in a home dir , path should end with "/" */
/* draw it using draw package by */
load(draw);
/* if graphic file is empty (= 0 bytes) then run draw2d command again */
draw2d(
terminal = 'svg,
file_name = sconcat(path,"t105"),
user_preamble="set size nosquare;set key top right",
title= "Circle arcs from points ",
dimensions = [1000, 1000],
yrange = [-2,2],
xrange = [-2,2],
xlabel = "zx ",
ylabel = "zy",
point_type = filled_circle,
points_joined =true,
color = green,
key = "arc1",
points(arc1),
color=red,
key = "arc2",
points(arc2)
);
lemniskata
edytujRysujemy lemniscatę
- w postaci uwikłanej:
load(implicit_plot); z:x+y*%i; f(n):=abs(z^n-1); implicit_plot (f(2) = 1, [x, -2, 2], [y, -2, 2]);
- w postaci parametrycznej
plot2d ([parametric, cos(t), sin(t)*cos(t), [t,-%pi,%pi],[nticks,80]], [x, -4/3, 4/3])$
Rysowanie zbioru punktów
edytuj
- tworzymy 2 listy:
- xx z wartościami x
- yy z wartościami yy
- wyświetlamy listy używając procedury draw2d z pakietu draw
load(draw); draw2d( points(xx,yy));
albo tworzymy 1 listę xy z parami wartości x i y i rysujemy:
load(draw); draw2d( points(xy));
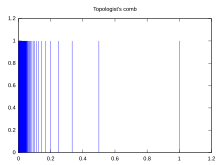
Topologiczny grzebień:
load(draw); /* by Mario Rodríguez Riotorto http://riotorto.users.sourceforge.net/gnuplot/index.html */ draw2d( title = "Topologist\\47s comb", /* Syntax for postscript enhanced option; character 47 = ' */ xrange = [0.0,1.2], yrange = [0,1.2], file_name = "comb2", terminal = svg, points_joined = impulses, /* vertical segments are drawn from points to the x-axis */ color = "blue", points(makelist(1/x,x,1,1000),makelist(1,y,1,1000)) )$
typ punktu
edytuj-1 $none 0 dot 1 plus 2 multiply 3 asterisk 4 square 5 filled_square 6 circle 7 filled_circle 8 up_triangle 9 filled_up_triangle 10 down_triangle 11 filled_down_triangle 12 diamant 13 filled_diamant
tablica
edytuj1D
edytujRysowanie danych w postaci tablicy[9]
array(a,5) $ for i:0 thru 5 do a[i]: bfloat(random(1.0))$
za pomocą plot2d:
plot2d( [discrete, listarray (a)] ) $
lub draw2d:
load(draw)$
draw2d(
points_joined=true,
points(listarray(a))) $
2D
edytuj- draw ( picture) [10]
Biblioteki graficzne
edytujZapisywanie grafiki do pliku
edytujterminal
edytuj- screen ( pozwala manipulować obrazami 3d i sprawdzić jak będzie wyglądała grafika
- svg
- png
Zapisywanie wykresu do pliku eps
edytujW przypadku Windows plik będzie w katalogu c:\
plot2d([f1(x),f2(x)],[x,0,1],[gnuplot_term,ps], [gnuplot_out_file,"log.eps"]);
Tworzenie pliku SVG
edytujBeginSVG(file_name,cm_width,cm_height,i_width,i_height):= block( destination : openw (file_name), printf(destination, "<?xml version=\"1.0\" encoding=\"UTF-8\" standalone=\"no\"?>~%"), printf(destination, "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"~%\"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">~%"), printf(destination,"<svg width=\"~d cm\" height=\"~d cm\" viewBox=\"0 0 ~d ~d\" xmlns=\"http://www.w3.org/2000/svg\" version=\"1.1\">~%", cm_width,cm_height,i_width,i_height), return(destination) ); CircleSVG(dest,center_x,center_y,_radius):=printf(dest,"<circle cx=\"~f\" cy=\"~f\" r=\"~f\" fill=\"white\" stroke=\"black\" stroke-width=\"2\"/>~%", center_x,center_y,_radius); CloseSVG(destination):= ( printf(destination,"</svg>~%"), close (destination) ); /* ---------------------------------------------------- */ cmWidth:10; cmHeight:10; iWidth:800; iHeight:600; radius:200; centerX:400; centerY:300; f_name:"b.svg"; /* ------------------------------------------------------*/ f:BeginSVG(f_name,cmWidth,cmHeight,iWidth,iHeight); CircleSVG(f,centerX,centerY,radius); CloseSVG(f);
Różnice między Maximą a innymi językami
edytujInstrukcja for
edytujW Maximie dozwolone jest użycie wartości niecałkowitych jako indeksów pętli for:
for x:0.5 step 0.001 thru 1.0 do
Indeks zmiennej for nie jest widoczny poza pętlą:
for i:1 thru 5 do print("inside i = ",i);
"inside i = "1
"inside i = "2
"inside i = "3
"inside i = "4
"inside i = "5
(%o1) done
(%i2) print(i);
i
(%o2) i
Zmienne lokalne funkcji
edytujZmienne lokalne musisz zadeklarować przed użyciem (porównaj konstrukcje w Lispie).
Problemy
edytuj- czytaj komunikaty
- wyłącz kompilację funkcji ( compile(all) )
- przekształc funkcje w ciąg instrukcji
- Informacje o błędach ( ang. Error messages) [11]
- informacje o ostrzeżeniach ( ang. Warning messages) [12]
nietypowy komunikat obłędzie
edytuj- sprawdź
- ostatnie edycje
- czy nie używasz nazwy zastrzeżonej ( korzystaj z indeku w dokumentacji Maximy )
- błędna nazwa ( literówka) funkcji powoduje wynik nie taki jak chcemy
Unable to evaluate predicate emtyp
edytujPrzyczyna: błędna nazwa funkcji : nie emtyp tylko emptyp
Display all 2857 possibilities? (y or n)
edytujPrzy kopiowaniu/wklejaniu kodu do linii poleceń pojawia się komunita:
Display all 2857 possibilities? (y or n)
Jest to komunikat funkcji readline z GCL.[13]
Rozwiązaniem jest używanie bash lub load do wprowadznia komend a nie wklejanie
gnuplot i util.c
edytujutil.c: No such file or directory
Problemem może być zła ścieżka/nazwa do pliku
incorrect syntax: Illegal use of delimiter )
edytuj- przykładowa przyczyna: niepotrzebny znak końca linii w ostatniej linii bloku
/* błędny przykład */ ( x:1, y:2, /* tutaj nie wolno dodawa c znaku końca linii */ ),
incorrect syntax: Missing )
edytujJeśli Maxima wyświetla definicję funkcji, to błąd jest w kodzie następnej funkcji, której Maxima nie wyświetla
"incorrect syntax: x is not an infix operator"
edytujPrzyczyna: brak znaku końca linii w linii poprzedzającej momemet wystąpienia błędu.
Rozwiazanie : dodać :
- $ lub ;
- , ( w obrębie bloku )
cons: 2nd argument must be a non-atomic expression;
edytujPrzyczyna: złą kolejność argumentów cons Rozwiązanie: zmian akolejności
(%i14) cons(a,[b,c,d]); (%o14) [a, b, c, d] (%i15) cons([b,c,d],a); cons: 2nd argument must be a non-atomic expression; found a -- an error. To debug this try: debugmode(true);
bind stack overflow
edytujJest to błąd Lispa
On August 17, 2014, Gunter Konigsmann wrote: > Bind stack overflow normally indicates that you > are using a recursive function that your lisp > didn't convert into a non-recursive loop or > that you are trying to handle numbers with > thousands of digits...
Przykadow przyczyny:
Bardzo długie wyrażenie symboliczne :
c: 0.5624000299307079*%i+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
+(0.5624000299307079*%i
Rozwiązanie :
- przekszatałecenie do wyrażeni anumerycznego : float(rectform(c))
Zobacz również
edytujŹródła
edytuj- ↑ askubuntu question : how-to-install-maxima-cas-on-ubuntu-21-04
- ↑ stackoverflow question : passing-a-parameter-to-the-function-in-maxima-cas
- ↑ stackoverflow question : array-to-matrix
- ↑ Graphical representation of complex numbers
- ↑ stackoverflow question : how-to-compute-derivative-in-maxima
- ↑ Discussion at Maxima interest list
- ↑ Macrakis - dyskuja na liście dyskusyjnej
- ↑ Maxima helpful hints. How do I plot a function which I defined?
- ↑ maxima-discuss: plotting data that is in an array
- ↑ 'draw'-Gnuplot interface: object image
- ↑ maxima manual : Error and warning messages
- ↑ maxima docs: Warning-messages
- ↑ stackoverflow question: function-definition-in-maxima-cas

