Astrofizyka/Kwantowy oscylator harmoniczny

Oscylator harmoniczny jest układem fizycznym, który ma duże zastosowanie i znaczenie w wielu działach fizyki.

Jest to ciało o masie m, na które działa siła proporcjonalna do wychylenia z przeciwnym zwrotem $F=-kx$. Ponieważ siła F= - ∂U/∂x, to układ opisany jest przez potencjał:

$U(x)={\frac {1}{2}}kx^{2}={\frac {1}{2}}m\omega ^{2}x^{2}.$

Jego energia całkowita jest równa:

$E={\frac {1}{2}}mv^{2}+U(x)={\frac {p^{2}}{2m}}+U(x)$

gdzie pęd p=mv. W mechanice kwantowej pęd p przechodzi w operator: p=mv⇒p= - iℏ ${\frac {d}{dx}}$ spełniający regułę komutacyjną [x,p]=iℏ. Wygodnie jest zdefiniować zamiast x, p dwa operatory

$a={\frac {1}{\sqrt {2}}}\left({\sqrt {\frac {m\omega }{\hbar }}}x+i{\frac {1}{\sqrt {m\omega \hbar }}}p\right),$ $a^{+}={\frac {1}{\sqrt {2}}}\left({\sqrt {\frac {m\omega }{\hbar }}}x-i{\frac {1}{\sqrt {m\omega \hbar }}}p\right)$

nazywane operatorami anihilacji i kreacji, stąd operator położenia x to

$x={\sqrt {\frac {\hbar }{2m\omega }}}(a+a^{+})$

Potencjał oscylatora harmonicznego i kilka pierwszych stanów własnych.

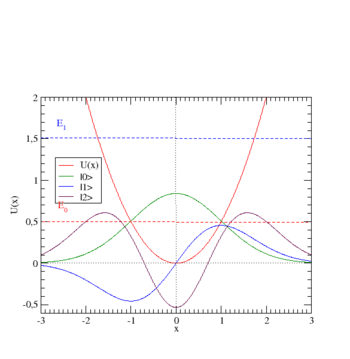
Bozonowy oscylator harmoniczny

Hamiltonian, czyli operator energii, przyjmuje teraz postać

$H={\frac {1}{2}}\hbar \omega (a^{+}a+aa^{+})$

Operatory $X_{i}$={I,a,$a^{+}$ ,n=$a^{+}a$} rozpinają algebrę Heisenberga: [a,$a^{+}$ ]=1, [a,a]=[$a^{+}$ ,$a^{+}$]=0, [n,a]= - a, [n,$a^{+}$ ]=$a^{+}$, [I,Xi]=0. Komutator zdefiniowany jest jako [A,B]=A B - B A a antykomutator {A,B}=A B + B A. Hamiltoniam można przekształcić do postaci:

$H=\hbar \omega \left(n+{\frac {1}{2}}\right)=\hbar \omega n+E_{0}$

gdzie $E_{0}={\frac {1}{2}}\hbar \omega$ jest energią stanu podstawowego. Hamiltoniam posiada całą drabinkę stanów własnych H|n> =$E_{n}$|n> z energiami własnymi:

$E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)=\hbar \omega n+E_{0}$

i stanami własnymi:

$|n>={\frac {1}{\sqrt {n!}}}(a^{+})^{n}|0>.$

Stan podstawowy |0> zdefiniowany jest jako a|0> =0. W tradycyjnym zapisie stan |n> opisuje funkcję falową $\psi _{n}(x)$. Równanie a|0>=0 (lub $a\psi _{0}(x)=0$) jest równaniem różniczkowym którego rozwiązaniem jest funkcja falowa stanu podstawowego:

$\psi _{0}=C_{0}\exp \left(-{\frac {1}{2}}{\left({\frac {x}{x_{0}}}\right)}^{2}\right)$

gdzie $x_{0}={\sqrt {\frac {\hbar }{m\omega }}}$. Operatory kreacji $a^{+}$ tworzą kolejne funkcje falowe stanów wzbudzonych (stąd ich nazwa – creare (łac.) to tworzyć). Można je wyrazić przez wielomian|wielomiany Hermite'a:

$\psi _{n}(x)={\frac {1}{\sqrt {n!}}}(a^{+})^{n}\psi _{0}(x)=C_{n}H_{n}\left({\frac {x}{x_{0}}}\right)\psi _{0}(x)$

gdzie

$H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}.$

Fermionowy oscylator harmoniczny

Fermionowy oscylator harmoniczny opisujemy hamiltonianem:

$H={\frac {1}{2}}\hbar \omega (c^{+}c-cc^{+})$

Operatory $X_{i}$={I,c,$c^{+}$ ,n=$c^{+}c$} rozpinają algebrę gradowaną: {c,$c^{+}$ }=1, {c,c}={$c^{+}$ ,$c^{+}$ }=0, [n,c]= - c, [n,$c^{+}$ ]=$c^{+}$, [I,$X_{i}$]=0. Hamiltonian ten można przekształcić do postaci

$H=\hbar \omega \left(n+{\frac {1}{2}}\right)=\hbar \omega n+E_{0}$

gdzie $E_{0}$= - ${\frac {1}{2}}$ℏω jest energią stanu podstawowego. Reguła komutacyjna {$c^{+},c^{+}$}=0 oznacza zakaz Pauliego, istnieje tylko stan próżni |0>, pierwszy stan wzbudzony |1>=$c^{+}$|0>, drugi stan wzbudzony już nie istnieje: |2>=$(c^{+})2|0>=0$, bo z reguł antykomatacyjnych wynika, iż $(c^{+})^{2}=0$. Fermionowy oscylator harmoniczny zbudowany jest tylko z dwóch stanów, stanu podstawowego |0> i stanu wzbudzonego |1>. Posiada tylko dwie wartości własne $E_{0}$= - ${\frac {1}{2}}$ℏω i $E_{1}$= ${\frac {1}{2}}$ℏω.

Supersymetria

Bozonowy i ferminowy hamiltonian razem posiada dodatkową symetrię, która miesza bozonowe stopnie swobody z fermionowymi – nazywamy ją supersymetrią,

$H={\frac {1}{2}}\hbar \omega (\{a^{+},a\}+[c^{+},c]\}).$

Generowana jest przez operatory: $Q={\sqrt {2\omega }}a^{+}c$, $Q^{+}={\sqrt {2\omega }}c^{+}a$, spełniają one relację:

$\{Q,Q^{+}\}=2H.$

Ta własność jest podstawą konstrukcji supersymetycznej teorii pola.