Fale/Opis fal biegnących

Opis fal biegnących

---

Licencja

Autor: Mirosław Makowiecki Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność.

---

---

Będziemy rozpatrywali tutaj układy otwarte, tzn. nie mające zewnętrznych granic. Powietrze na dworze dla rozchodzących się fal dźwiękowych zachowuje się jak układ otwarty, pomijamy tutaj efekty powstałe dotyczące odbić fal dźwiękowych od budynków. Rozchodzące się fale dźwiękowe w zamkniętym pomieszczeniu zachowuje się jak układ zamknięty. Jeśli ścianki tego pomieszczenia pokryjemy materiałem całkowicie pochłaniających fale dźwiękowe, to wtedy taki układ zachowuje się jak układ otwarty. Rozpatrzmy tutaj fale, których wychylenia od stanu równowagi piszemy:

$\psi (0,t)=A\cos \omega t\;$

(4.1)

Rozpatrzmy układ, który zachowuje się jak w punkcie z=0 w czasie t', który piszemy w zależności od "t" i położenia, w której rozchodzi się fala z prędkością fazową v_f:

$t^{'}=t-{{z} \over {v_{f}}}\;$

(4.2)

Wzór (4.2) możemy podstawić do wzoru (4.1), w ten sposób otrzymać równość zależną od czasu i położenia zetowego "z", w której znajduje się fala biegnąca:

$\psi (z,t)=\psi (0,t^{'})=A\cos \omega t^{'}=A\cos \omega \left(t-{{z} \over {v_{f}}}\right)=A\cos \left(\omega t-{{\omega z} \over {v_{f}}}\right)\;$

(4.3)

Dla fal bięgnących, która jest funkcją kosinus, zapisaną w zależności od liczby falowej i częstotliwości kołowej, przestawiamy wzorem:

$\psi (z,t)=A\cos(\omega t-kz)\;$

(4.4)

Możemy porównać wzór (4.4) ze wzorem (4.3), które oznaczają to samo, w ten sposób dostajemy wniosek, że liczba falowa jest stosunkiem częstotliwości kołowej drgań harmonicznych i prędkości fazowej drgań:

$k={{\omega } \over {v_{f}}}\;$

(4.5)

co z (4.5) możemy napisać definicję prędkości fazowej w zależności od częstotliwości kołowej i liczby falowej, która jest ich stosunkiem, w tej samej linijce napiszmy dwa następne wzory określającą prędkość fazowa, która za pierwszym razem jest iloczynem długości falowej i częstotliwości, a za drugim razem jest stosunkiem liczby falowej przez okres drgań fal biegnących:

$v_{f}={{\omega } \over {k}}\;$

(4.6)

$v_{f}=\lambda \nu \;$

(4.7)

$v_{f}={{\lambda } \over {T}}\;$

(4.8)

Zdefiniujemy funkcję fazową, która jest zdefiniowana w zależności od częstotliwości kołowej i liczby falowej, a także od zmiennych czasu "t" i położenia "z":

$\varphi (z,t)=\omega t-kz\;$

(4.9)

Podamy teraz inną metodę wyprowadzenia wzoru na prędkość fazową, zatem na podstawie definicji funkcji fazowej (4.9), której różniczka jest napiszemy z definicji różniczki zupełnej, którą wyrazimy w zależności od częstotliwości kołowej ω i liczby falowej "k":

$d\varphi ={{\partial \varphi } \over {\partial t}}dt+{{\partial \varphi } \over {\partial z}}dz=\omega dt-kdz\;$

(4.10)

Rozpatrzmy, gdy różniczka funkcji fazowej jest równa dokładnie zero, w ten sposób dostajemy równość z definicji prędkości znaną z kinematyki klasycznej, którą nazwiemy prędkością fazową:

$v_{f}=\left({{dz} \over {dt}}\right)_{\varphi =\operatorname {const} }={{\omega } \over {k}}\;$

(4.11)

Związek dyspersyjny dla wahadeł matematycznych sprzężonych przy pomocy sprężynek

Równanie różnicowo-różniczkowe możemy napisać wzorem (2.86), które dla porządku dziennego tutaj przepisujemy:

${\ddot {\psi }}_{n}=-{{g} \over {l}}\psi _{n}+{{K} \over {M}}\left(\psi _{n+1}-\psi _{n}\right)-{{K} \over {M}}(\psi _{n}-\psi _{n-1})\;$

(4.12)

Dla fal biegnących, którego wychylenie od stanu równowagi jest opisane w punkcie (4.4), dla której drugą pochodną cząstkową względem czasu piszemy:

${\ddot {\psi }}_{n}=-\omega ^{2}\psi _{n}\;$

(4.13)

Równanie (4.12) możemy zapisać, przy pomocy zachodzącej tożsamości dla fal biegnących (4.13), która jest drugą pochodną cząstkową wychylenia podłużnego względem czasu, która jest iloczynem wychylenia od stanu równowagi ψ_n przez kwadrat częstotliwości kołowej drgań i to wszystko wzięte z minusem:

$\omega ^{2}={{g} \over {l}}+{{2K} \over {M}}\left(1-{{\psi _{n+1}+\psi _{n-1}} \over {2\psi _{n}}}\right)\;$

(4.14)

Harmoniczne fale biegnące

Dla fal sinusoidalnych fal biegnących wychylenie od stanu równowagi możemy przepisać w zależności od częstotliwości kołowej i liczby falowej w zależności od zmiennej czasowej i położenia z=na:

$\psi _{n}=A\cos(\omega t+\varphi -kz)\;$

(4.15)

Suma wychyleń (4.15) dla n+1 i n-1 piszemy przy pomocy wychylenia od stanu równowagi dla n w sposób:

$\psi _{n+1}+\psi _{n-1}=A\cos(\omega t+\varphi +kna+ka)+A\cos(\omega t+\varphi +kna-ka)=2\psi _{n}\cos ka\;$

(4.16)

Związek (4.16) możemy podstawić do (4.13), w ten sposób dostajemy związek dyspersyjny na kwadrat częstotliwości kołowej w zależności od liczby falowej w postaci:

$\omega ^{2}={{g} \over {l}}-{{2K} \over {M}}\sin ^{2}{{ka} \over {2}}\;$

(4.17)

Eksponencjalne fale biegnące w układzie otwartym

Dla fal eksponencjalnych biegnących w układzie otwartym wychylenie od stanu równowagi dla z=na zależnego od częstotliwości kołowej i stałej zaniku fal χ, piszemy:

$\psi (z,t)=Ae^{-\chi z}\cos \omega t\;$

(4.18)

Suma wychyleń (4.18) dla n+1 i n-1 piszemy przy pomocy wychylenia od stanu równowagi dla n w sposób:

$\psi _{n+1}+\psi _{n-1}=Ae^{-\chi kna}e^{-\chi ka}\cos \omega t+Ae^{\chi ka}e^{\chi na}\cos \omega t=Ae^{-\chi kna}\cos \omega t\left(e^{\chi ka}+e^{-\chi ka}\right)=\psi _{n}\left(e^{\chi ka}+e^{-\chi ka}\right)\;$

(4.19)

Tożsamość napisana w punkcie (4.19) podstawiamy do (4.13), przy wykorzystaniu definicji funkcji hiperbolicznych, w ten sposób mamy związek dyspersyjny na kwadrat częstotliwości kołowej względem wielkości stałej zaniku dla rozchodzących się fal biegnących eksponencjalnych:

$\omega ^{2}=\omega _{0}^{2}-{{4K} \over {M}}\sinh ^{2}{{\chi a} \over {2}}\;$

(4.20)

Przemienne eksponencjalne fale biegnące w układzie otwartym

Dla fal eksponencjalnych biegnących w układzie otwartym wychylenie od stanu równowagi, dla z=na zależnego od częstotliwości kołowej i stałej zaniku fal χ, piszemy w postaci:

$\psi (z,t)=A(-1)^{n}e^{-\chi z}\cos \omega t\;$

(4.21)

Suma wychyleń (4.21) dla n+1 i n-1 piszemy przy pomocy wychylenia od stanu równowagi dla n:

$\psi _{n+1}+\psi _{n-1}=-A(-1)^{n}e^{-\chi kna}e^{-\chi ka}\cos \omega t-Ae^{\chi ka}(-1)^{n}e^{\chi na}\cos \omega t=-Ae^{-\chi kna}(-1)^{n}\cos \omega t\left(e^{\chi ka}+e^{-\chi ka}\right)=-\psi _{n}\left(e^{\chi ka}+e^{-\chi ka}\right)\;$

(4.22)

Tożsamość napisana w punkcie (4.22) podstawiamy do (4.13), przy wykorzystaniu definicji funkcji hiperbolicznych, w ten sposób mamy związek dyspersyjny na kwadrat częstotliwości kołowej w zależności od stałej zaniku χ dla rozchodzących się fal biegnących:

$\omega ^{2}=\omega _{0}^{2}+{{4K} \over {M}}\cosh ^{2}{{\chi a} \over {2}}\;$

(4.23)

Prędkość fazowa fal poprzecznych rozchodzącej się w strunie obciążonymi ciężarkami

Prędkość fazowa rozchodzenia się fal w strunie obciążonej sprężynkami możemy napisać patrząc na definicję kwadratu częstotliwości kołowej (2.71), z którego wyznaczymy samą częstotliwość, co po podzieleniu jego obustronnie przez liczbę falową "k" otrzymamy prędkość fazową:

$v_{f}={{\omega } \over {k}}=2{\sqrt {{T_{0}} \over {Ma}}}{{\sin {{ka} \over {2}}} \over {k}}\;$

(4.24)

Biorąc przypadek dla małej liczby falowej "k", wtedy obliczenia dla wzoru (4.24) przeprowadzamy tak jak w punkcie (2.77), w ten sposób możemy otrzymać wzór na prędkość fazową w przybliżeniu małej liczby falowej wykorzystując przy tym definicję masowej gęstości liniowej, zatem dokonajmy tychże obliczeń:

$v_{f}={\sqrt {{T_{0}a} \over {M}}}={\sqrt {{T_{0}a} \over {M}}}{{\sin {{ka} \over {2}}} \over {{ka} \over {2}}}={\sqrt {{T_{0}a} \over {M}}}{{{{ka} \over {2}}-{{1} \over {6}}\left({{ka} \over {2}}\right)^{3}+...} \over {{ka} \over {2}}}={\sqrt {{T_{0}a} \over {M}}}\left(1-{{1} \over {24}}(ka)^{2}+...\right)\simeq {\sqrt {{T_{0}a} \over {M}}}={\sqrt {{T_{0}} \over {\rho _{0}}}}\;$

(4.25)

Prędkość fazowa fal podłużnych rozchodzącej się w strunie obciążonymi ciężarkami

Prędkość rozchodzenia się fal w zależności liczby falowej możemy przestawić wykorzystując wzór na kwadrat częstotliwości kołowej (2.79) z którego wyznaczymy samą częstotliwość, co po podzieleniu jego przez liczbę falową "k", w ten sposób dostajemy wzór na prędkość fazową rozchodzenia się fal:

$v_{f}={{\omega } \over {k}}=2{\sqrt {{K} \over {M}}}{{\sin {{ka} \over {2}}} \over {k}}\;$

(4.26)

Dokonując podobnych obliczeń jak w punkcie (4.25) dla k bardzo małego, w ten sposób wykorzystując definicję gęstości liniowej, by otrzymać później tożsamość:

$v_{f}={\sqrt {{Ka^{2}} \over {M}}}{{\sin {{ka} \over {2}}} \over {{ka} \over {2}}}\simeq {\sqrt {{Ka^{2}} \over {M}}}={\sqrt {{Ka} \over {\rho _{0}}}}={\sqrt {{K_{L}L} \over {\rho _{0}}}}\;$

(4.27)

bo zachodzi K_LL=Ka, w którym każda sprężyna ma współczynnik sprężystości równej K, sprężynki wszystkie razem wzięte mają współczynnik sprężystości K_L i dlatego tak powinniśmy napisać.

Prędkość rozchodzenia się dźwięku w naczyniu

Będziemy tutaj wyprowadzać równanie rządzącego przy rozchodzącego się dźwięku w danym ośrodku znając pochodną zupełną ciśnienia względem objętości w stanie równowagi danego ośrodka, tutaj będziemy się zajmować powietrzem, ale związek , który tutaj otrzymamy jest zgodny dla innych ośrodków sprężystych a także dla powietrza. Powietrze znajdujące się w naczyniu zachowuje się jak sprężynka o stałej sprężystości K_L, którego długość jest L₁, która zostaje ściśnięta do długości L, a siła wywierana na ścianki naczynia jest wyrażona wzorem:

$F=-K_{L}(L-L_{1})\;$

(4.28)

Możemy zróżniczkować tożsamość (4.28), w ten sposób otrzymać równość różniczkową:

$dF=-K_{L}dL\;$

(4.29)

Z drugiej jednak strony powiedźmy, gdy nastąpi zmiana długości sprężyny dL towarzyszy zmiana ciśnienia dp i zmiana siły wywieranej dF, zatem tą siłę piszemy:

$dF=Adp=A\left({{dp} \over {dV}}\right)_{0}AdL=A^{2}\left({{dp} \over {dV}}\right)dL\;$

(4.30)

Porównując wzory (4.30) z (4.29) możemy napisać tożsamość na współczynnik sprężystości powietrza:

$K_{L}=-A^{2}{{dp} \over {dV}}\;$

(4.31)

Gęstość liniową masy możemy powiązać z gęstością objętościową, która jak udowodnimy gęstość liniowa masy jest równa iloczynowi gęstości objętościowej pomnożonej przez powierzchnię przekroju ośrodka, w której dźwięk rozchodzi się względem linii prostopadłej względem tego przekroju, według związku:

$\rho _{0L}L_{0}=\rho _{0V}AL_{0}\Rightarrow \rho _{0L}=\rho _{0V}A\;$

(4.32)

Wzory (4.31) i (4.32) możemy podstawić do wzoru końcowego (4.25), w ten sposób otrzymujemy końcową równość na kwadrat prędkości rozchodzenia się dźwięku:

$v^{2}={{K_{L}L} \over {\rho _{0L}}}=\left({{-A^{2}{{dp} \over {dV}}L} \over {\rho _{0V}A}}\right)=-{{-AL\left({{dp} \over {dV}}\right)_{0}} \over {\rho _{0V}}}=-{{V_{0}} \over {\rho _{0}}}\left({{dp} \over {dV}}\right)_{0}\;$

(4.33)

Prędkość rozchodzenia się fal w powietrzu

Biorąc równanie stanu gazu doskonałego dla izotermy, czyli pod stałą temperaturą, wyznaczać z niego będziemy ciśnienie panujące w panujące gazie w zależności od jej objętości:

$pV=p_{0}V_{0}\Rightarrow p={{p_{0}V_{0}} \over {V}}\;$

(4.34)

Wyznaczmy teraz pierwszą pochodną zupełną ciśnienia (4.34) względem objętości V i kładąc V=V₀:

${{dp} \over {dV}}=-{{p_{0}V_{0}} \over {V^{2}}}\Rightarrow V_{0}\left({{dp} \over {dV}}\right)_{0}=-p_{0}\;$

(4.35)

Wzór (4.35) podstawiamy do (4.33), w ten sposób dostajemy równość, którą wyrażamy w zależności od ciśnienia gazu i jego gęstości objętościowej:

$v={\sqrt {{p_{0}} \over {\rho _{0}}}}\;$

(4.36)

Poprawka do modelu dotyczącego prędkości rozchodzenia się dźwięku

Model opisujący prędkość dźwięku w gazie opisaną w punkcie (4.36) jest modelem tylko dobrym, tylko jest jedyna różnica, że w tym modelu prędkość dźwięku jest napisana z błędem 15% w porównaniem z prędkością dźwięku policzonego z doświadczenia, zatem ten model zawiera pewne błędy, który świadczy, że zastosowaliśmy model gazu doskonałego dla stałej temperatury układu. Lepszym modelem jest równanie adiabaty. W porównaniu modelu Boyla i adiabaty przy sprężaniu gazu ciśnienie jest nieco większe a przy rozprężaniu jest nieco mniejsze. Podczas rozprężaniu i sprężenia gazu temperatura gazu nie jest w rzeczywiści stała w danym punkcie przestrzeni. Biorąc równanie stanu gazu doskonałego dla adiabaty, czyli układu nie wymieniającego się energii z otoczeniem, wyznaczać z niego będziemy ciśnienie panujące w gazie w zależności od jej objętości:

$pV^{\kappa }=p_{0}V_{0}^{\kappa }\Rightarrow p=p_{0}V_{0}^{\kappa }V^{-\kappa }\;$

(4.37)

Wyznaczmy teraz pierwszą pochodną zupełną ciśnienia (4.38) względem objętości V i kładąc V=V₀, by w ten sposób otrzymać równość:

${{dp} \over {dv}}=-\kappa p_{0}V_{0}^{\kappa }V^{-\kappa -1}\Rightarrow V_{0}\left({{dp} \over {dV}}\right)_{0}=-\kappa p_{0}\;$

(4.38)

Wzór (4.38) podstawiamy do (4.33), w ten sposób otrzymać równość na prędkość fazową rozchodzenia się fal dźwiękowych, którą wyrażamy w zależności od ciśnienia gazu i jego gęstości objętościowej, która panuje w stanie równowagi:

$v={\sqrt {{\kappa p_{0}} \over {\rho _{0}}}}\;$

(4.39)

Prędkość fazowa w linii przesyłowym

Częstotliwość fazową linii przesyłowej możemy przestawić poprzez wzór (2.84), który możemy przestawić w granicy małych liczb falowych w postaci:

$\omega ^{2}={{4} \over {LC}}\sin ^{2}{{ka} \over {2}}\simeq {{4} \over {LC}}{{k^{2}a^{2}} \over {4}}={{a^{2}k^{2}} \over {LC}}\;$

(4.40)

Kwadrat prędkości fazowej przestawiamy z jego definicji (4.11) dla małych liczb falowych, która jest przestawiona jako odwrotność iloczynu ilorazu indukcji własnej przez przez długość linii przez iloraz pojemności linii przez jej długość:

$v_{f}^{2}={{\omega ^{2}} \over {k^{2}}}={{{a^{2}k^{2}} \over {LC}} \over {k^{2}}}={{a^{2}} \over {LC}}={{1} \over {{{L} \over {a}}{{C} \over {a}}}}\;$

(4.41)

Dolnoprzepustowa linia przesyłowa

(Rys. 4.1) Dolno przepustowa linia cylindryczna

Z prawa Gaussa dla elektrostatyki, w zależności od ładunku znajdującego się wewnętrznej powierzchni możemy opisać z tego prawa wniosek:

$-E\epsilon _{0}2\pi ra=Q\Rightarrow E=-{{Q} \over {2\pi \epsilon _{0}ra}}\;$

(4.42)

Wyznaczmy teraz różnicę potencjału między dolną częścią a jej górną częścią kondensatora, którą możemy przestawić według obliczeń:

$-{{d\varphi } \over {dr}}=-{{Q} \over {2\pi \epsilon _{0}ra}}\Rightarrow d\varphi ={{Q} \over {2\pi \epsilon _{0}ra}}dr\Rightarrow U={{Q} \over {2\pi \epsilon _{0}a}}\ln {{r+D} \over {r}}\;$

(4.43)

Całkowita pojemność kondensatora (4.41) jest przestawiana z jego definicji jako iloraz ładunku na okładkach kondensatora cylindrycznego przez jego różnicę potencjałów pomiędzy cylindrycznymi okładkami:

$C={{Q} \over {U}}={{2\pi \epsilon _{0}a} \over {\ln {{r+D} \over {r}}}}\;$

(4.44)

Wyznaczmy indukcję magnetyczną pola magnetycznego znajdującego się w kondensatorze pomiędzy jego okładkami:

$B2\pi r=\mu _{0}I\Rightarrow B={{\mu _{0}I} \over {2\pi r}}\;$

(4.45)

Policzmy strumień indukcji pola magnetycznego z jego formalnej definicji, a później indukcję własną:

$\Phi =\int _{r}^{r+D}Bdra=a\int _{r}^{r+D}{{\mu _{0}I} \over {2\pi r}}dr={{\mu _{0}aI} \over {2\pi }}\ln {{r+D} \over {r}}\Rightarrow L={{\mu _{0}a} \over {2\pi }}\ln {{r+D} \over {r}}\;$

(4.46)

Napiszmy teraz iloczyn pojemności elektrycznej kondensatora C i indukcyjności z jej definicji, tzn. (4.42) i (4.43):

$LC={{2\pi \epsilon _{0}a} \over {\ln {{r+D} \over {r}}}}{{\mu _{0}a} \over {2\pi }}\ln {{r+D} \over {r}}=\mu _{0}\epsilon _{0}a^{2}\Rightarrow {{C} \over {a}}{{L} \over {a}}={{1} \over {c^{2}}}\;$

(4.47)

Jeśli popatrzymy na wzór na kwadrat prędkości fazowej (4.41) i na wzór (4.47) dowiadujemy się, że prędkość fazowa jest równa prędkości światła w dolnoprzepustowej linii przesyłowej.

Linia przesyłowa zrobiona przy pomocy dwóch równoległych pasków przewodzących

(Rys. 4.2) Linia przesyłowa zbudowana przy pomocy równoległych pasków przewodzących

Różnica potencjałów między paskami określamy z jego definicji, a także natężenie pola elektrycznego określamy z prawa Gaussa, piszemy je związkami:

$U=gE_{x}\;$

(4.48)

$E_{x}={{Q} \over {\epsilon _{0}wa}}\;$

(4.49)

Pojemność elektryczna, która jest ilorazem ładunku znajdującego na kondensatorze przez różnicę potencjału znajdującego się na okładkach, wyraża się:

$C={{Q} \over {U}}={{Q} \over {gE_{x}}}={{Q} \over {g{{Q} \over {\epsilon _{0}wa}}}}\Rightarrow {{C} \over {a}}={{w\epsilon _{0}} \over {g}}\;$

(4.50)

Strumień indukcji pola magnetycznego względem powierzchni bocznej możemy określić jako iloczyn igrekowej współrzędnej indukcji pola magnetycznego przez powierzchnię o wartości ga:

$\Phi =B_{y}ga\;$

(4.51)

Z prawa Stokesa możemy również powiedzieć, że iloczyn współrzędnej igrekowej pola magnetycznego i długości bocznej kondensatora jest równa iloczynowi przenikalności magnetycznej ośrodka, w którym jest próżnia, przez natężenie prądu elektrycznego płynącego w linii:

$wB_{y}=\mu _{0}I\Rightarrow B_{y}=\mu _{0}{{I} \over {w}}\;$

(4.52)

Wzór na indukcję pola magnetycznego a właściwie na jej współrzędną igrekową podstawiamy do (4.51), wykorzystując definicję indukcyjności własnej, możemy pisać:

$\Phi =LI=\mu _{0}{{Iga} \over {w}}\Rightarrow {{L} \over {a}}={{\mu _{0}g} \over {w}}\;$

(4.53)

Mnożymy wzory (4.50) i (4.53), w ten sposób otrzymujemy odwrotność na kwadrat prędkości światła w próżni:

${{C} \over {a}}{{L} \over {a}}={{w\epsilon _{0}} \over {g}}{{\mu _{0}g} \over {w}}=\mu _{0}\epsilon _{0}={{1} \over {c^{2}}}\;$

(4.54)

Patrząc wzór na kwadrat prędkości fazowej (4.41) i definicję iloczynu ilorazu pojemności linii przesyłowej przez "a" i przez iloraz indukcji pola magnetycznego przez "a". dowiadujemy się, że prędkość fazową linii przesyłowej jest równa prędkości światła w próżni "c".

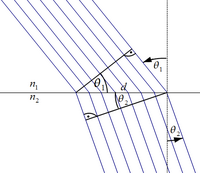
Zjawisko załamania światła i dyspersja

(Rys. 4.3) Zjawisko załamania promieni świetlnych

Z rysunku obok otrzymujemy natychmiast, następujące dwa równania, które wynikają z rysunku obok:

${{v_{1}t} \over {d}}=\sin \theta _{1}\;$

(4.55)

${{v_{2}t} \over {d}}=\sin \theta _{2}\;$

(4.56)

Dzielimy wzory (4.55) i (4.56) względem siebie, dostajemy:

${{v_{1}} \over {v_{2}}}={{\sin \theta _{1}} \over {\sin \theta _{2}}}\Rightarrow {{c} \over {v_{1}}}\sin \theta _{1}={{c} \over {v_{2}}}\sin \theta \;$

(4.57)

Teraz wykorzystamy definicję współczynnika załamania n=c/v dla rozważanego ośrodka pierwszego i drugiego, to na podstawie tego równość (4.57) przepisujemy jako:

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\;$

(4.58)

Wyprowadzenie wzoru na współczynnik załamania promieni świetlnych

Względna przenikalność elektryczną możemy przepisać według następującego schematu:

${\vec {D}}=\epsilon _{0}{\vec {E}}+{\vec {P}}\;$

(4.59)

Dalszym krokiem jest wyprowadzenie wzoru na współczynnik przenikalność elektryczną względną, wiedząc że $_{{\vec {P}}=\chi \epsilon _{0}{\vec {E}}}\;$, którego przestawienie jest:

$\epsilon _{r}\epsilon _{0}{\vec {E}}=\epsilon _{0}{\vec {E}}+\epsilon _{0}\chi {\vec {E}}\Rightarrow \epsilon _{r}=1+\chi \;$

(4.60)

Na podstawie alternatywnej definicji polaryzacji elektrycznej P=Nqx(t) przenikalność względna elektryczna możemy przepisać do:

$\epsilon _{r}=1+{{Nqx(t)} \over {\epsilon _{0}E(t)}}\;$

(4.61)

Napiszmy teraz równanie ruchu ładunku elektrycznego, który napiszemy za pomocą częstotliwości drgań podstawowych ω₀, współczynnika tłumienia Γ, i przy pomocy natężenia pola elektrycznego zmieniającego się według funkcji kosinus E(t)=E₀cosωt, wtedy:

$M{\ddot {x}}=-M\omega _{0}^{2}-M\Gamma {\dot {x}}+qE(t)\;$

(4.62)

Położenie ciała o masie M możemy zapisać jako rozwiązanie równania (4.62) przy pomocy amplitudy elastycznej A_el i absorpcyjnej A_ab według:

$x(t)=A_{el}\cos \omega t+A_{ab}\cos \omega t\;$

(4.63)

Rozważmy sobie ośrodek przezroczysty, takich jak szkło, woda, są one przezroczyste i nie następuje wtedy absorpcja promieni świetlnych. Dla ośrodków barwnych, nastepuje absorpcja wszystkich częstości oprócz jednej, i interesują nam te częstości, które są daleko od częstości rezonansowych, wtedy amplituda absorpcyjna według (3.29) jest w przybliżeniu równa zero, zatem istnieje tylko amplituda elastyczna, która jest równa dla naszego przypadku według (3.30):

$n^{2}={{c^{2}} \over {v^{2}}}={{c^{2}} \over {{c^{2}} \over {\mu _{r}\epsilon _{r}}}}=\mu _{r}\epsilon _{r}\simeq \epsilon _{r}=1+{{Nqx(t)} \over {\epsilon _{0}E(t)}}=1+{{Nq^{2}} \over {\epsilon _{0}M}}{{1} \over {\omega _{0}^{2}-\omega ^{2}}}\;$

(4.64)

Powyżej skorzystano z definicji współczynnika załamania, a także z definicji prędkości światła w ośrodku materialnym, dla którego względna przenikalność magnetyczna jest w przybliżeniu równa jeden. Jeśli powiązać kwadrat współczynnika załamania z liczbą falową, z częstotliwością kołową i z prędkością światła w próżni, to wtedy wzór (4.64) jest w postaci:

${{c^{2}k^{2}} \over {\omega ^{2}}}=n^{2}=\epsilon _{r}=1+{{Nq^{2}} \over {\epsilon _{0}M}}{{1} \over {\omega _{0}^{2}-\omega ^{2}}}\;$

(4.65)

Związek (4.65) jest związkiem liczby falowej z częstotliwością kołową, który jest związkiem dyspersyjnych dla światła widzialnego.

Strumień energii i impedancja

Prędkość fazową rozchodzenia się fal w strunie obciążonych punktowymi ciężarkami określamy jako pierwiastek z stosunku siły napięcia działająca na strunę T₀ i gęstości liniowej struny ρ₀, a impedancję charakterystyczną nazywamy pierwiastek z iloczynu gęstości liniowej struny i siły napięcia, których definicje tychże wielkości określamy poprzez wzory:

$v_{f}={\sqrt {{T_{0}} \over {\rho _{0}}}}\;$

(4.66)

$Z={\sqrt {\rho _{o}T_{0}}}\;$

(4.67)

Poniżej podamy również wzór na impedancję w tej samej strunie, ale dla drgań poprzecznych.

Fale poprzeczne biegnące w strunie ciągłej

Całkowita siła iksowa działająca na ciągłą strunę wywołująca jego ruch falowy w postaci fal biegnących określamy przez:

$F_{x}=T\sin \theta =T\cos \theta {{\sin \theta } \over {\cos \theta }}=T_{0}\operatorname {tg} \theta =T_{0}{{\partial \psi } \over {\partial z}}\;$

(4.68)

Wprowadzenie do definicji impedancji charakterystycznej

Każdy element struny ciągłej wykonuje ruch harmoniczny określanych jako funkcja, dla której jest ona wprost proporcjonalna do kosinusa z argument różnicy iloczynu częstotliwości kołowej przez czas i iloczynu liczby falowej przez położenie danego elementu struny, co jego definicja tejże funkcji piszemy przez:

$\psi (z,t)=A\cos(\omega t-kz)\;$

(4.69)

Pierwsza pochodna wychylenia od stanu równowagi ψ(z,t) względem położenia z i czasu t struny piszemy przez:

${{\partial \psi } \over {\partial z}}=kA\sin(\omega t-kz)\;$

(4.70)

${{\partial \psi } \over {\partial t}}=-\omega A\sin(\omega t-kz)\;$

(4.71)

(Rys. 4.4) Wytwarzanie fal biegnących. a) równowaga, b)ogólna konfiguracja

Patrząc na wzory (4.70) i (4.71) możemy napisać wzór łączący pochodną cząstkową wychylenia od stanu równowagi (4.43) względem położenia z i pochodnej cząstkową wychylenia względem czasu w sposób:

${{\partial \psi } \over {\partial z}}=-{{1} \over {v_{f}}}{{\partial \psi } \over {\partial t}}\;$

(4.72)

Całkowita siła działająca na strunę ze strony generatora (4.66) możemy napisać wykorzystując wniosek (4.72), wtedy:

$F_{x}=-{{T_{0}} \over {v_{f}}}{{\partial \psi } \over {\partial t}}\;$

(4.73)

Wprowadźmy teraz impedancję, jest ona stosunkiem siły T₀ i prędkości fazowej:

$Z={{T_{0}} \over {v_{f}}}={{T_{0}} \over {\sqrt {{T_{0}} \over {\rho _{0}}}}}={\sqrt {T_{0}\rho _{0}}}\;$

(4.74)

Przy definicji impedancji (4.74) wzór na siłę iksowa działającą na strunę ciągłą określamy jako iloczyn pochodnej cząstkowej wychylenia od stanu równowagi ψ względem czasu "t" przez impedancję Z, to razem wszystko wzięte z minusem:

$F_{x}=-Z{{\partial \psi } \over {\partial t}}\;$

(4.75)

Moc wytwarzana przez generator drgań struny

Całkowita wytwarzana moc w czasie "t" jest iloczynem siły F_x zdefiniowaną w punkcie (4.75) i prędkości wychylenia od stanu równowagi, która jest pochodną cząstkową wychylenia ψ względem czasu:

$P(t)=F_{x}{{\partial \psi } \over {\partial t}}=\left(Z{{\partial \psi } \over {\partial t}}\right){{\partial \psi } \over {\partial t}}=Z\left({{\partial \psi } \over {\partial t}}\right)^{2}\;$

(4.76)

Innym sposobem wyprowadzenie mocy wytwarzanej przez generator jest opisany przez wzór w zależności od pierwszej pochodnej cząstkowej wychylenia względem położenia:

$P(t)=F_{x}{{\partial \psi } \over {\partial t}}=\left[-T_{0}{{\partial \psi } \over {\partial z}}\right]{{\partial \psi } \over {\partial t}}=\left[-T_{0}{{\partial \psi } \over {\partial z}}\right]\left[-v_{f}{{\partial \psi } \over {\partial z}}\right]={{v_{f}} \over {T_{0}}}\left[-T_{0}{{\partial \psi } \over {\partial z}}\right]^{2}={{1} \over {Z}}\left[-T_{0}{{\partial \psi } \over {\partial z}}\right]^{2}\;$

(4.77)

Promieniowanie wytarzane przez układ sprężynek i mas

(Rys. 4.5) Emisja promieniowania fal podłużnych przez generator. a)Równowaga. b) układ w ruchu.

Niech mamy układ sprężynek, które łączą jednakowe masy, wtedy wielkość odpowiadająca wielkości napięcia w strunie T₀ jest wielkość Ka, wtedy impedancję możemy określić jako pierwiastek z wielkości Ka i gęstości masowej liniowej:

$Z={{Ka} \over {\sqrt {{Ka} \over {\rho _{0}}}}}={\sqrt {Ka\rho _{0}}}\;$

(4.78)

Całkowita moc wytwarzana przez generator podczas wytwarzania fal podłużnych w układzie sprężynek w zależności od czasu "t" lub położenia jest pisana:

$P(z,t)=Z\left[{{\partial \psi (z,t)} \over {\partial t}}\right]^{2}={{1} \over {Z}}\left[-Ka{{\partial \psi (z,t)} \over {\partial z}}\right]^{2}\;$

(4.79)

Całkowita siła działająca na układ mas sprężynek przy założeniu, że w stanie równowagi sprężynki pozostają napięte z siłą F₀, która nie wpływa na ruch drgający układów kulek, jest określona:

$F_{x}=F_{0}-Ka{{\partial \psi (z,t)} \over {\partial z}}\;$

(4.80)

Fale głosowe

Prędkość fazowa fal dźwiękowej jest określana przez wzór (4.39), porównując ten wzór z (4.27) (w tym drugim mamy gęstość liniową, a w tym pierwszym gęstość objętościową), dochodzimy do wniosku, że rolę napięcia sprężyny spełnia κp₀, wtedy impedancję piszemy:

$Z={\sqrt {\kappa p_{0}\rho _{0}}}\;$

(4.81)

Natężenia fali dźwiękowej można napisać na podstawie tożsamości (4.77) określoną względem pochodnej wychylenia podłużnego ψ(z,t) względem czasu "t" lub położenia "z":

$I(z,t)=Z\left[{{\partial \psi (z,t)} \over {\partial t}}\right]^{2}={{1} \over {Z}}\left[-\kappa p_{0}{{\partial \psi (z,t)} \over {\partial z}}\right]^{2}\;$

(4.82)

Siłą działająca na jednostkę powierzchni określamy względem stałego ciśnienia panującego w ośrodku p₀, która to fala dźwiękowa zaburza stałe nasze ciśnienie atmosferyczne przy pomocy członu harmonicznego, który powoduje, że mamy raz ciśnienie wyższe, a za drugim niższe od naszego rozważanego ciśnienia p₀.

${{F_{x}} \over {A}}=p_{0}-\kappa p_{0}{{\partial \psi (z,t)} \over {\partial z}}\;$

(4.83)