Matematyka ubezpieczeń życiowych/Podstawowe ubezpieczenia życiowe

Podobnie jak w przypadku teorii oprocentowania, rozpoczniemy od najprostszych ubezpieczeń w których kwota świadczenia jest równa $1$. Znamy kwotę jaką otrzymamy. Tym więc o co będziemy pytać będzie wartość obecna tego świadczenia. Będziemy więc zastanawiać się nad tym ile trzeba zapłacić jednorazowo (bez uwzględnienia kosztów ubezpieczyciela) by uzyskać dane ubezpieczenie. Kwotę taką będziemy nazywać jednorazową składką netto (NSP – Net Single Premium) Wartość obecna netto ubezpieczeń na życie jest oznaczana literą $A$ z odpowiednimi indeksami określającymi typ ubezpieczenia.

Oznaczmy przez $Z$ wartość obecną wartością obecną netto (NPV – Net Present Value) świadczenia wypłacanego z tytułu danej polisy. Ustalając wartość obecną netto ubezpieczenia nie możemy posłużyć się wzorami deterministycznymi ponieważ są one uzależnione od czynnika losowego. By dokonać wyceny netto ubezpieczenia musimy posłużyć się wartością oczekiwaną zmiennej losowej $Z$. Postępowanie takie jest uzasadnione wnioskami płynącymi z prawa wielkich liczb. Suma wielu realizacji zmiennej losowej $Z$ będzie wraz ze wzrostem ich liczby $n$ dążyć do $n\cdot E(Z)$ a zatem kwota potrzebna na wypłatę świadczeń dużej liczbie ubezpieczonych będzie w przybliżeniu równa wartości oczekiwanej takiej wypłaty przemnożonej przez liczbę wystawionych polis.

Ubezpieczenia na życie według momentu wypłaty świadczenia dzieli się na:

• płatne na koniec roku śmierci
• płatne w chwili śmierci
• płatne na koniec podokresu roku śmierci (miesiąc, kwartał)

Ze względu na okres odpowiedzialności ubezpieczeniowej, ubezpieczenia można podzielić na:

• ubezpieczenia na życie, bezterminowe
• ubezpieczenia na życie, terminowe
• ubezpieczenia na dożycie
• ubezpieczenia na życie i dożycie
• odroczone ubezpieczenia na życie, bezterminowe
• odroczone ubezpieczenia na życie, terminowe

Oprócz ubezpieczeń na kwotę jednostkową rozważa się jeszcze ubezpieczenia:

• rosnące (kwota świadczenia wzrasta o 1 co roku)
• malejące (kwota świadczenia maleje o 1 co roku)

przy czym zmiana wysokości świadczenia może następować w sposób ciągły lub skokowy w okresach rocznych lub podokresach.

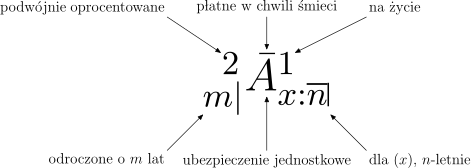
Powyższy rysunek ilustruje sposób odczytywania symboli aktuarialnych.

Ubezpieczenia płatne na koniec roku śmierci

Ozn.	$E(Z)\;$	$Var(Z)=E(Z^{2})-E^{2}(Z)\;$	$Z\;$
$A_{x}\;$	$\sum \limits _{k=0}^{\infty }v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$	${}^{2}A_{x}-A_{x}^{2}\;$	$v^{k+1}\quad {\text{dla }}k=0,1,\ldots \;$
$A_{x:{\overline {n}}|}^{1}\;$	$\sum \limits _{k=0}^{n-1}v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$	${}^{2}A_{x:{\overline {n}}|}^{1}-\left(A_{x:{\overline {n}}|}^{1}\right)^{2}\;$	${\begin{cases}v^{k+1}&{\text{dla }}k=0,1,\ldots ,n-1\\0&{\text{dla }}k=n,n+1,n+2,\ldots \end{cases}}\;$
$A_{x:{\overline {n}}|}^{\;\;\;1}\;$	$v^{n}{}_{n}p_{x}\;$	${}^{2}A_{x:{\overline {n}}|}^{\;\;\;1}-\left(A_{x:{\overline {n}}|}^{\;\;\;1}\right)^{2}\;$	${\begin{cases}0&{\text{dla }}k=0,1,\ldots ,n-1\\v^{n}&{\text{dla }}k=n,n+1,n+2,\ldots \end{cases}}\;$
$A_{x:{\overline {n}}|}\;$	$A_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}\;$	${}^{2}A_{x:{\overline {n}}|}-\left(A_{x:{\overline {n}}|}\right)^{2}\;$	${\begin{cases}v^{k+1}&{\text{dla }}k=0,1,\ldots ,n-1\\v^{n}&{\text{dla }}k=n,n+1,n+2,\ldots \end{cases}}\;$
${}_{m|n}A_{x}\;$	$A_{x:{\overline {n}}|}^{1}-A_{x:{\overline {m}}|}^{1}\;$	${}_{m|n}^{\;\;\;2}A_{x}-\left({}_{m|n}A_{x}\right)^{2}\;$	${\begin{cases}0&{\text{dla }}k=0,1,\ldots ,m-1\\v^{k+1}&{\text{dla }}k=m,m+1,m+2,\ldots ,m+n-1\\0&{\text{dla }}k=m+n,m+n+1,\ldots \end{cases}}\;$
${}_{m|}A_{x}\;$	$A_{x}-A_{x:{\overline {m}}|}^{1}\;$	${}_{m|}^{\;\;\;2}A_{x}-\left({}_{m|}A_{x}\right)^{2}\;$	${\begin{cases}0&{\text{dla }}k=0,1,\ldots ,m-1\\v^{k+1}&{\text{dla }}k=m,m+1,m+2,\ldots \\\end{cases}}\;$
$(IA)_{x:{\overline {n}}|}^{1}\;$	$\sum \limits _{k=0}^{n-1}(k+1)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		${\begin{cases}(k+1)v^{k+1}&{\text{dla }}k=0,1,\ldots ,n-1\\0&{\text{dla }}k=n,n+1,n+2,\ldots \end{cases}}\;$
$(DA)_{x:{\overline {n}}|}^{1}\;$	$\sum \limits _{k=0}^{n-1}(n-k)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		${\begin{cases}(n-k)v^{K+1}&{\text{dla }}k=0,1,\ldots ,n-1\\0&{\text{dla }}k=n,n+1,n+2,\ldots \end{cases}}\;$
$(IA)_{x}\;$	$\sum \limits _{k=0}^{\infty }(k+1)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		$(k+1)v^{k+1}\quad {\text{dla }}k=0,1,\ldots \;$

Ubezpieczenia płatne w chwili śmierci

Ozn.	$E(Z)\;$	$Var(Z)=E(Z^{2})-E^{2}(Z)\;$	$Z\;$
${\bar {A}}_{x}\;$	$\int \limits _{0}^{\infty }v^{t}{}_{t}p_{x}\mu _{x+t}dt\;$	${}^{2}{\bar {A}}_{x}-{\bar {A}}_{x}^{2}\;$	$v^{t}\quad {\text{dla }}t\in (0,+\infty )\;$
${\bar {A}}_{x:{\overline {n}}|}^{1}\;$	$\int \limits _{0}^{n}v^{t}{}_{t}p_{x}\mu _{x+t}dt\;$	${}^{2}{\bar {A}}_{x:{\overline {n}}|}^{1}-\left({\bar {A}}_{x:{\overline {n}}|}^{1}\right)^{2}\;$	${\begin{cases}v^{t}&{\text{dla }}t\in (0,n]\\0&{\text{dla }}t\in (n,+\infty )\end{cases}}\;$
$A_{x:{\overline {n}}|}^{\;\;\;1}\;$	$v^{n}{}_{n}p_{x}\;$	${}^{2}A_{x:{\overline {n}}|}^{\;\;\;1}-\left(A_{x:{\overline {n}}|}^{\;\;\;1}\right)^{2}\;$	${\begin{cases}0&{\text{dla }}t\in (0,n]\\v^{n}&{\text{dla }}t\in (n,+\infty )\end{cases}}\;$
${\bar {A}}_{x:{\overline {n}}|}\;$	${\bar {A}}_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}\;$	${}^{2}{\bar {A}}_{x:{\overline {n}}|}-\left({\bar {A}}_{x:{\overline {n}}|}\right)^{2}\;$	${\begin{cases}v^{t}&{\text{dla }}t\in (0,n]\\v^{n}&{\text{dla }}t\in (n,+\infty )\end{cases}}\;$
${}_{m|n}{\bar {A}}_{x}\;$		${}_{m|n}^{\;\;\;2}A_{x}-\left({}_{m|n}A_{x}\right)^{2}\;$	${\begin{cases}0&{\text{dla }}t\in (0,n]\\v^{n}&{\text{dla }}t\in (n,n+m]\\0&{\text{dla }}t\in (m+n,+\infty )\end{cases}}\;$
$({\bar {I}}{\bar {A}})_{x:{\overline {n}}|}^{1}\;$	$\int \limits _{0}^{n}tv^{t}{}_{t}\,p_{x}\mu _{x+t}dt\;$		${\begin{cases}[t+1]v^{t}&{\text{dla }}t\in (0,n]\\0&{\text{dla }}t\in (n,+\infty )\end{cases}}\;$
$({\bar {D}}{\bar {A}})_{x:{\overline {n}}|}^{1}\;$	$\int \limits _{0}^{n}(n-t)v^{t}{}_{t}\,p_{x}\mu _{x+t}dt\;$		${\begin{cases}(n-[t])v^{t}&{\text{dla }}t\in (0,n]\\0&{\text{dla }}t\in (n,+\infty )\end{cases}}\;$
$({\bar {I}}{\bar {A}})_{x}\;$	$\int \limits _{0}^{\infty }tv^{t}{}_{t}\,p_{x}\mu _{x+t}dt\;$		$tv^{t}\quad {\text{dla }}t>0\;$

Zależności

Wzorów zaprezentowanych poniżej nie będziemy dowodzić. Ograniczymy się jedynie do krótkich interpretacji ułatwiających zapamiętanie.

$A_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}=A_{x:{\overline {n}}|}$

Interpretacja: Ubezpieczenie na życie i dożycie jest sumą ubezpieczenia na życie i ubezpieczenia na dożycie.

$A_{x}=vq_{x}+vp_{x}\cdot A_{x+1}$

Interpretacja: Ubezpieczony $(x)$ może umrzeć w ciągu najbliższego roku (z prawdopodobieństwem $q_{x}$) i otrzymać świadczenie w wysokości $1$, lub przeżyć najbliższy rok (z prawdopodobieństwem $p_{x}$) i być ubezpieczonym $x+1$-latkiem z ubezpieczeniem o wartości $A_{x+1}$. Będzie to za rok więc dyskontujemy czynnikiem dyskontującym $v$.

$A_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}\cdot A_{x+n}=A_{x}$

Interpretacja: Jest to uogólnienie zależności opisanej powyżej. (Pamiętajmy, że $A_{x:{\overline {n}}|}^{\;\;\;1}=v^{n}{}_{n}p_{x}$ jest czynnikiem dyskontującym w sensie aktuarialnym tj. z uwzględnieniem prawdopodobieństwa przeżycia.)

$(IA)_{x}=A_{x}+vp_{x}\cdot (IA)_{x+1}$

Interpretacja: Ubezpieczenie o rosnącej kwocie świadczenia zawiera w sobie zwykłe ubezpieczenie na życie. Ponadto po roku dodatkowo pojawia się ubezpieczenie z kwotą rosnącą startującą od jedynki.

$(IA)_{x:{\overline {n}}|}^{1}+(DA)_{x:{\overline {n}}|}^{1}=(n+1)\cdot A_{x:{\overline {n}}|}^{1}$

Interpretacja: Sumy kwot wypłat z tytułu ubezpieczenia z świadczeniem malejącym i rosnącym są w każdym roku jednakowe i równe $n+1$.

Przy założeniu UDD prawdziwe są zależności:

${\bar {A}}_{x}={\frac {i}{\delta }}A_{x},\;$

${\bar {A}}_{x:{\overline {n}}|}^{1}={\frac {i}{\delta }}A_{x:{\overline {n}}|}^{1}.\;$

Dla ubezpieczeń na życie i dożycie analogiczna zależność nie zachodzi

${\bar {A}}_{x:{\overline {n}}|}={\bar {A}}_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}={\frac {i}{\delta }}A_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}^{\;\;\;1}=\left({\frac {i}{\delta }}-1\right)A_{x:{\overline {n}}|}^{1}+A_{x:{\overline {n}}|}.\;$

Funkcje komutacyjne dla podstawowych ubezpieczeń

W dzisiejszych czasach przechowywanie dużej ilości danych i wykonywanie na nich obliczeń nie stanowi kłopotu za sprawą komputerów. Dawniej jednak istotne znaczenie miało aby dane niezbędne do skalkulowania składki dały się wydrukować na sensownej liczbie stron a sama kalkulacja nie nastręczała zbyt dużych trudności rachunkowych. Nie można więc było tworzyć tablicy zawierającej dane dla każdego wieku i każdego okresu ubezpieczenia. Wymyślono więc funkcje komutacyjne. Mają one obecnie znaczenie jedynie w dydaktyce matematyki ubezpieczeniowej.

Przyjmuje się następujące oznaczenia

${\begin{aligned}D_{x}&:=v^{x}l_{x}\\C_{x}&:=v^{x+1}d_{x}\\M_{x}&:=\sum _{k=0}^{\infty }C_{x+k}\\R_{x}&:=\sum _{k=0}^{\infty }M_{x+k}=\sum _{k=0}^{\infty }(k+1)C_{x+k}\end{aligned}}$

Wtedy wartości aktuarialne poszczególnych ubezpieczeń oblicza się następująco

${\begin{aligned}A_{x}&:={\frac {M_{x}}{D_{x}}}\\A_{x:{\overline {n}}|}^{1}&:={\frac {M_{x}-M_{x+n}}{D_{x}}}\\A_{x:{\overline {n}}|}^{\,\,\,1}&:={\frac {D_{x+n}}{D_{x}}}\\A_{x:{\overline {n}}|}&:={\frac {M_{x}-M_{x+n}+D_{x+n}}{D_{x}}}\end{aligned}}$